Bài viết hướng dẫn giải các bài tập trong phần câu hỏi và bài tập và phần luyện tập của sách giáo khoa Giải tích 12 cơ bản: Tích phân.CÂU HỎI VÀ BÀI TẬPBài 1. Tính các tích phân sau đây:
a) $int_{ – frac{1}{2}}^{frac{1}{2}} {sqrt[3]{{{{(1 – x)}^2}}}} dx.$
b) $int_0^{frac{pi }{2}} {sin } left( {frac{pi }{4} – x} right)dx.$
c) $int_{frac{1}{2}}^2 {frac{1}{{x(x + 1)}}dx} .$
d) $int_0^2 x {(x + 1)^2}dx.$
e) $int_{frac{1}{2}}^2 {frac{{1 – 3x}}{{{{(x + 1)}^2}}}dx} .$
f) $int_{ – frac{pi }{2}}^{frac{pi }{2}} {sin } 3x.cos 5xdx.$Lời giải:
a) Đặt $u = 1 – x$ ta có $du = – dx.$
Khi $x = – frac{1}{2}$ thì $u = frac{3}{2}$; khi $x = frac{1}{2}$ thì $u = frac{1}{2}.$
Do đó: $int_{ – frac{1}{2}}^{frac{1}{2}} {sqrt[3]{{{{(1 – x)}^2}}}dx} $ $ = – int_{frac{3}{2}}^{frac{1}{2}} {sqrt[3]{{{u^2}}}} du$ $ = int_{frac{1}{2}}^{frac{3}{2}} {{u^{frac{2}{3}}}} du$ $ = left. {frac{3}{5}{u^{frac{5}{3}}}} right|_{frac{1}{2}}^{frac{3}{2}}$ $ = left. {frac{3}{5}usqrt[3]{{{u^2}}}} right|_{frac{1}{2}}^{frac{3}{2}}.$
$ = frac{3}{5}left( {frac{3}{2}sqrt[3]{{frac{9}{4}}} – frac{1}{2}sqrt[3]{{frac{1}{4}}}} right)$ $ = frac{3}{{10sqrt[3]{4}}}(3sqrt[3]{9} – 1).$
b) Đặt $u = frac{pi }{4} – x$ ta có $du = – dx.$
Khi $x = 0$ thì $u = frac{pi }{4}$; khi $x = frac{pi }{2}$ thì $u = – frac{pi }{4}.$
Do đó: $int_0^{frac{pi }{2}} {sin } left( {frac{pi }{4} – x} right)dx$ $ = – int_{frac{pi }{4}}^{ – frac{pi }{4}} {sin udu} $ $ = int_{ – frac{pi }{4}}^{frac{pi }{4}} {sin udu} $ $ = – left. {cos u} right|_{ – frac{pi }{4}}^{frac{pi }{4}}$ $ = – left( {cos frac{pi }{4} – cos left( { – frac{pi }{4}} right)} right) = 0.$
Vậy $int_0^{frac{pi }{2}} {sin } left( {frac{pi }{4} – x} right)dx = 0.$
c) Ta có: $frac{1}{{x(x + 1)}} = frac{1}{x} – frac{1}{{x + 1}}.$
Do đó: $int_{frac{1}{2}}^2 {frac{{dx}}{{x(x + 1)}}} $ $ = int_{frac{1}{2}}^2 {left( {frac{1}{x} – frac{1}{{x + 1}}} right)dx} $ $ = int_{frac{1}{2}}^2 {frac{{dx}}{x}} – int_{frac{1}{2}}^2 {frac{{dx}}{{x + 1}}} $ $ = int_{frac{1}{2}}^2 {frac{{dx}}{x}} – int_{frac{1}{2}}^2 {frac{{d(x + 1)}}{{x + 1}}} $ $ = left. {ln |x|} right|_{frac{1}{2}}^2 – left. {ln |x + 1|} right|_{frac{1}{2}}^2.$
$ = ln 2 – ln frac{1}{2} – ln 3 – ln frac{3}{2}$ $ = ln 2.$
d) $int_0^2 x {(x + 1)^2}dx$ $ = int_0^2 {left( {{x^3} + 2{x^2} + x} right)dx} $ $ = left. {left( {frac{{{x^4}}}{4} + frac{2}{3}{x^3} + frac{1}{2}{x^2}} right)} right|_0^2$ $ = 4 + frac{{16}}{3} + 2$ $ = frac{{34}}{3}.$
e) Đặt $u = x + 1$ ta có $du = dx$ và $x = u – 1.$
Khi $x = frac{1}{2}$ thì $u = frac{3}{2}$; khi $x = 2$ thì $u = 3.$
Do đó: $int_{frac{1}{2}}^2 {frac{{1 – 3x}}{{{{(x + 1)}^2}}}dx} $ $ = int_{frac{3}{2}}^3 {frac{{1 – 3(u – 1)}}{{{u^2}}}du} $ $ = int_{frac{3}{2}}^3 {frac{{4 – 3u}}{{{u^2}}}du} $ $ = 4int_{frac{3}{2}}^3 {frac{{du}}{{{u^2}}}} – 3int_{frac{3}{2}}^3 {frac{{du}}{u}} $ $ = – left. {frac{4}{u}} right|_{frac{3}{2}}^3 – left. {3ln u} right|_{frac{3}{2}}^3.$
$ = – left( {frac{4}{3} – frac{4}{{frac{3}{2}}}} right) – 3left( {ln 3 – ln frac{3}{2}} right)$ $ = frac{4}{3} – 3ln 2.$
f) Ta có: $sin 3x.cos 5x$ $ = frac{1}{2}(sin 8x – sin 2x).$
Do đó: $int_{ – frac{pi }{2}}^{frac{pi }{2}} {sin } 3x.cos 5xdx$ $ = frac{1}{2}int_{ – frac{pi }{2}}^{frac{pi }{2}} {(sin 8x – sin 2x)dx} $ $ = frac{1}{2}int_{ – frac{pi }{2}}^{frac{pi }{2}} {sin 8xdx} – frac{1}{2}int_{ – frac{pi }{2}}^{frac{pi }{2}} {sin 2xdx} .$
$ = left. { – frac{1}{{16}}cos 8x} right|_{ – frac{pi }{2}}^{frac{pi }{2}} + left. {frac{1}{4}cos 2x} right|_{ – frac{pi }{2}}^{frac{pi }{2}}$ $ = – frac{1}{{16}}[cos 4pi – cos ( – 4pi )]$ $ + frac{1}{4}[cos pi – cos ( – pi )].$
$ = – frac{1}{{16}}(1 – 1) + frac{1}{4}( – 1 + 1) = 0.$Bài 2. Tính các tích phân sau:
a) $int_0^2 {|1 – x|dx} .$
b) $int_0^{frac{pi }{2}} {{{sin }^2}xdx} .$
c) $int_0^{ln 2} {frac{{{e^{2x + 1}} + 1}}{{{e^x}}}dx.} $
d) $int_0^pi {sin 2x.{{cos }^2}xdx.} $Lời giải:
a) Ta có: $|1 – x|$ $ = left{ {begin{array}{*{20}{l}}
{1 – x:{rm{ với }}:0 le x le 1}\
{x – 1:{rm{ với }}:1 le x le 2}
end{array}} right..$
Do đó:
$int_0^2 {|1 – x|dx} $ $ = int_0^1 {(1 – x)dx} + int_1^2 {(x – 1)dx} $ $ = left. {left( {x – frac{{{x^2}}}{2}} right)} right|_0^1 + left. {left( {frac{{{x^2}}}{2} – x} right)} right|_1^2$ $ = frac{1}{2} + frac{1}{2} = 1.$
b) Ta có: ${sin ^2}x = frac{{1 – cos 2x}}{2}.$
Do đó: $int_0^{frac{pi }{2}} {{{sin }^2}xdx} $ $ = frac{1}{2}int_0^{frac{pi }{2}} {(1 – cos 2x)dx} $ $ = frac{1}{2}int_0^{frac{pi }{2}} {dx} – frac{1}{2}int_0^{frac{pi }{2}} {cos 2xdx} $ $ = left. {frac{1}{2}x} right|_0^{frac{pi }{2}} – left. {frac{1}{4}sin 2x} right|_0^{frac{pi }{2}}$ $ = frac{pi }{4}.$
c) $int_0^{ln 2} {frac{{{e^{2x + 1}} + 1}}{{{e^x}}}dx} $ $ = int_0^{ln 2} {left( {{e^{x + 1}} + {e^{ – x}}} right)dx} $ $ = int_0^{ln 2} {{e^{x + 1}}} dx + int_0^{ln 2} {{e^{ – x}}} dx.$
$ = int_0^{ln 2} {{e^{x + 1}}} d(x + 1) – int_0^{ln 2} {{e^{ – x}}} d( – x)$ $ = left. {{e^{x + 1}}} right|_0^{ln 2} – left. {{e^{ – x}}} right|_0^{ln 2}.$
$ = {e^{ln 2 + 1}} – {e^1} – {e^{ – ln 2}} + 1$ $ = {e^{ln 2 + 1}} – frac{1}{{{e^{ln 2}}}} – (e – 1)$ $ = e + frac{1}{2}.$
d) $int_0^pi {sin 2x.{{cos }^2}xdx} $ $ = 2int_0^pi {sin x.{{cos }^3}xdx} $ $ = – 2int_0^pi {{{cos }^3}xd(cos x)} $ $ = – left. {2.frac{1}{4}{{cos }^4}x} right|_0^pi .$
$ = – frac{1}{2}left( {{{cos }^4}pi – {{cos }^4}0} right) = 0.$Bài 3. Sử dụng phương pháp đổi biến số, hãy tính:
a) $int_0^3 {frac{{{x^2}}}{{{{(1 + x)}^{frac{3}{2}}}}}dx} .$
b) $int_0^1 {sqrt {1 – {x^2}} } dx.$
c) $int_0^1 {frac{{{e^x}(1 + x)}}{{1 + x{e^x}}}dx.} $
d) $int_0^{frac{a}{2}} {frac{1}{{sqrt {{a^2} – {x^2}} }}dx} $ $(a > 0).$Lời giải:
a) Đặt $u = 1 + x$ ta có $du = dx$; ${x^2} = {(u – 1)^2}.$
Khi $x = 0$ thì $u = 1$; khi $x = 3$ thì $u = 4.$
Do đó: $int_0^3 {frac{{{x^2}}}{{{{(1 + x)}^{frac{3}{2}}}}}dx} $ $ = int_1^4 {frac{{{{(u – 1)}^2}}}{{{u^{frac{3}{2}}}}}du} $ $ = int_1^4 {frac{{{u^2} – 2u + 1}}{{{u^{frac{3}{2}}}}}du} .$
$ = int_1^4 {left( {{u^{frac{1}{2}}} – 2{u^{ – frac{1}{2}}} + {u^{ – frac{3}{2}}}} right)du} $ $ = int_1^4 {{u^{frac{1}{2}}}} du – 2int_1^4 {{u^{ – frac{1}{2}}}} du + int_1^4 {{u^{ – frac{3}{2}}}} du.$
$ = left. {frac{2}{3}{u^{frac{3}{2}}}} right|_1^4 – left. {4{u^{frac{1}{2}}}} right|_1^4 – left. {2{u^{ – frac{1}{2}}}} right|_1^4$ $ = frac{{16}}{3} – frac{2}{3} – (8 – 4) – 2left( {frac{1}{2} – 1} right)$ $ = frac{{14}}{3} – 3$ $ = frac{5}{3}.$
b) Cách 1: Đặt $x = sin t$ ta có: $dx = cos tdt.$
Khi $x = 0$ thì $t = 0$; khi $x = 1$ thì $t = frac{pi }{2}.$
Do đó: $int_0^1 {sqrt {1 – {x^2}} } dx$ $ = int_0^{frac{pi }{2}} {sqrt {1 – {{sin }^2}t} } cos tdt$ $ = int_0^{frac{pi }{2}} | cos t|.cos tdt$ $ = int_0^{frac{pi }{2}} {{{cos }^2}tdt} $ (vì $cos t ge 0$, $forall t in left[ {0;frac{pi }{2}} right]$).
$ Rightarrow int_0^1 {sqrt {1 – {x^2}} } dx$ $ = int_0^{frac{pi }{2}} {{{cos }^2}tdt} $ $ = frac{1}{2}int_0^{frac{pi }{2}} {(1 + cos 2t)dt} .$
$ = frac{1}{2}int_0^{frac{pi }{2}} {dt} + frac{1}{4}int_0^{frac{pi }{2}} {cos 2td(2t)} $ $ = left. {frac{1}{2}t} right|_0^{frac{pi }{2}} + left. {frac{1}{4}sin 2t} right|_0^{frac{pi }{2}}$ $ = frac{pi }{4} + 0 = frac{pi }{4}.$
Vậy $int_0^1 {sqrt {1 – {x^2}} } dx = frac{pi }{4}.$
Cách 2: Ta có $y = sqrt {1 – {x^2}} $, $0 le x le 1$ là phương trình của cung của đường tròn tâm $O$, bán kính $R = 1.$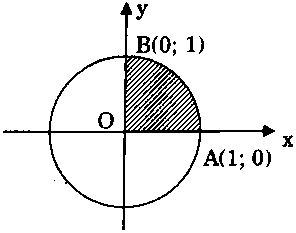
Vậy tích phân $int_0^1 {sqrt {1 – {x^2}} } dx$ bằng diện tích hình phẳng giới hạn bởi cung $AB$ và hai trục tọa độ. Hình phẳng đó là một phần tư đường tròn bán kính $1$, do đó: $int_0^1 {sqrt {1 – {x^2}} } dx = frac{pi }{4}.$
c) Đặt $u = x{e^x}$ ta có: $du = left( {{e^x} + x{e^x}} right)dx$ $ = {e^x}(x + 1)dx.$
Khi $x = 0$ thì $u = 0$; khi $x = 1$ thì $u = e.$
Do đó: $int_0^1 {frac{{{e^x}(x + 1)}}{{1 + x{e^x}}}dx} $ $ = int_0^e {frac{{du}}{{1 + u}}} $ $ = left. {ln (1 + u)} right|_0^e$ $ = ln (e + 1).$
d) Đặt $x = asin t$ ta có: $dx = acos tdt.$
Khi $x = 0$ thì $t = 0$; khi $x = frac{a}{2}$ thì $t = frac{pi }{6}.$
Do đó: $int_0^{frac{a}{2}} {frac{1}{{sqrt {{a^2} – {x^2}} }}dx} $ $ = int_0^{frac{pi }{6}} {frac{{acos tdt}}{{sqrt {{a^2} – {a^2}{{sin }^2}t} }}} $ $ = int_0^{frac{pi }{6}} {frac{{acos tdt}}{{|acos t|}}} .$
Vì $a > 0$ và $cos t ge 0$, $forall t in left[ {0;frac{pi }{6}} right]$ nên $int_0^{frac{pi }{6}} {frac{{acos tdt}}{{|a.cos t|}}} $ $ = int_0^{frac{pi }{6}} d t = left. t right|_0^{frac{pi }{6}} = frac{pi }{6}.$
Vậy $int_0^{frac{a}{2}} {frac{1}{{sqrt {{a^2} – {x^2}} }}dx} = frac{pi }{6}.$Bài 4. Sử dụng phương pháp tích phân từng phần hãy tính:
a) $int_0^{frac{pi }{2}} {(x + 1)} sin xdx.$
b) $int_1^e {{x^2}} ln xdx.$
c) $int_0^1 {ln } (1 + x)dx.$
d) $int_0^1 {left( {{x^2} – 2x – 1} right){e^{ – x}}dx} .$Lời giải:
a) Đặt $left{ {begin{array}{*{20}{l}}
{u = x + 1}\
{dv = sin xdx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = dx}\
{v = – cos x}
end{array}} right..$
Áp dụng công thức tính tích phân từng phần ta có:
$int_0^{frac{pi }{2}} {(x + 1)} sin xdx$ $ = – left. {(x + 1)cos x} right|_0^{frac{pi }{2}} + int_0^{frac{pi }{2}} {cos xdx} .$
$ = – left[ {left( {frac{pi }{2} + 1} right)cos frac{pi }{2} – cos 0} right] + left. {sin x} right|_0^{frac{pi }{2}}$ $ = 2.$
b) Đặt $left{ {begin{array}{*{20}{l}}
{u = ln x}\
{dv = {x^2}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{{dx}}{x}}\
{v = frac{{{x^3}}}{3}}
end{array}} right..$
Áp dụng công thức tính tích phân từng phần ta có:
$int_1^e {{x^2}} ln xdx$ $ = left. {frac{{{x^3}}}{3}ln x} right|_1^e – frac{1}{3}int_1^e {{x^2}} dx$ $ = frac{{{e^3}}}{3} – left. {frac{1}{9}{x^3}} right|_1^e$ $ = frac{{{e^3}}}{3} – frac{1}{9}left( {{e^3} – 1} right)$ $ = frac{2}{9}{e^3} + frac{1}{9}.$
c) Đặt $left{ {begin{array}{*{20}{l}}
{u = ln (1 + x)}\
{dv = dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{{1 + x}}dx}\
{v = x}
end{array}} right.$
Ta có: $int_0^1 {ln } (1 + x)dx$ $ = left. {xln (1 + x)} right|_0^1 – int_0^1 {frac{x}{{1 + x}}dx.} $
$ = ln 2 – int_0^1 {frac{{x + 1 – 1}}{{1 + x}}dx} $ $ = ln 2 – int_0^1 d x + int_0^1 {frac{{dx}}{{1 + x}}} .$
$ = ln 2 – left. x right|_0^1 + left. {ln (1 + x)} right|_0^1$ $ = ln 2 – 1 + ln 2$ $ = 2ln 2 – 1.$
d) Đặt $left{ {begin{array}{*{20}{l}}
{u = {x^2} – 2x – 1}\
{dv = {e^{ – x}}dx}
end{array}} right.$$ Rightarrow left{ {begin{array}{*{20}{l}}
{du = (2x – 2)dx}\
{v = – {e^{ – x}}}
end{array}} right..$
Áp dụng công thức tính tích phân từng phần ta có:
$int_0^1 {left( {{x^2} – 2x – 1} right){e^{ – x}}dx} $ $ = – left. {{e^{ – x}}left( {{x^2} – 2x – 1} right)} right|_0^1$ $ + int_0^1 {(2x – 2){e^{ – x}}dx} $ $ = frac{2}{e} – 1 + 2int_0^1 {(x – 1){e^{ – x}}dx.} $
Tiếp tục đặt: $left{ {begin{array}{*{20}{l}}
{{u_1} = x – 1}\
{d{v_1} = {e^{ – x}}dx}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{d{u_1} = du}\
{{v_1} = – {e^{ – x}}}
end{array}} right..$
Ta có: $int_0^1 {(x – 1){e^{ – x}}dx} $ $ = – left. {{e^{ – x}}(x – 1)} right|_0^1 + int_0^1 {{e^{ – x}}} dx$ $ = – 1 – left. {{e^{ – x}}} right|_0^1$ $ = – 1 – frac{1}{e} + 1$ $ = – frac{1}{e}.$
Vậy $int_0^1 {left( {{x^2} – 2x – 1} right){e^{ – x}}dx} $ $ = frac{2}{e} – 1 – frac{2}{e} = – 1.$ Bài 5. Tính các tích phân sau:
a) $int_0^1 {{{(1 + 3x)}^{frac{3}{2}}}dx} .$
b) $int_0^{frac{1}{2}} {frac{{{x^3} – 1}}{{{x^2} – 1}}dx.} $
c) $int_1^2 {frac{{ln (1 + x)}}{{{x^2}}}dx} .$Lời giải:
a) Đặt $u = 1 + 3x$ ta có: $du = 3dx.$
Khi $x = 0$ thì $u = 1$; khi $x = 1$ thì $u = 4.$
Do đó: $int_0^1 {{{(1 + 3x)}^{frac{3}{2}}}} dx$ $ = frac{1}{3}int_1^4 {{u^{frac{3}{2}}}} du$ $ = left. {frac{1}{3}.frac{2}{5}{u^{frac{5}{2}}}} right|_1^4$ $ = frac{2}{{15}}left( {{4^{frac{5}{2}}} – 1} right)$ $ = frac{{62}}{{15}}.$
b) $int_0^{frac{1}{2}} {frac{{{x^3} – 1}}{{{x^2} – 1}}dx} $ $ = int_0^{frac{1}{2}} {frac{{(x – 1)left( {{x^2} + x + 1} right)}}{{(x – 1)(x + 1)}}dx} $ $ = int_0^{frac{1}{2}} {frac{{{x^2} + x + 1}}{{x + 1}}dx} $ $ = int_0^{frac{1}{2}} {left( {x + frac{1}{{x + 1}}} right)dx.} $
$ = left. {frac{{{x^2}}}{2}} right|_0^{frac{1}{2}} + left. {ln (x + 1)} right|_0^{frac{1}{2}}$ $ = frac{1}{8} + ln frac{3}{2}.$
c) Đặt $left{ {begin{array}{*{20}{l}}
{u = ln (1 + x)}\
{dv = frac{{dx}}{{{x^2}}}}
end{array}} right.$ $ Rightarrow left{ {begin{array}{*{20}{l}}
{du = frac{1}{{1 + x}}dx}\
{v = – frac{1}{x}}
end{array}} right..$
Ta có: $int_1^2 {frac{{ln (1 + x)}}{{{x^2}}}dx} $ $ = – left. {frac{1}{x}ln (1 + x)} right|_1^2 + int_1^2 {frac{{dx}}{{x(1 + x)}}} $ $ = – frac{1}{2}ln 3 + ln 2 + int_1^2 {frac{{dx}}{{x(1 + x)}}} .$
Xét $int_1^2 {frac{{dx}}{{(x + 1)x}}} .$ Ta có: $frac{1}{{x(1 + x)}} = frac{1}{x} – frac{1}{{x + 1}}.$
Do đó: $int_1^2 {frac{{dx}}{{x(x + 1)}}} $ $ = int_1^2 {left( {frac{1}{x} – frac{1}{{x + 1}}} right)dx} $ $ = int_1^2 {frac{{dx}}{x}} – int_1^2 {frac{{dx}}{{x + 1}}} $ $ = left. {ln x} right|_1^2 – left. {ln (1 + x)} right|_1^2.$
$ = ln 2 – ln 3 + ln 2.$
Vậy $int_1^2 {frac{{ln (1 + x)}}{{{x^2}}}dx} $ $ = – frac{1}{2}ln 3 + ln 2 + ln 2 – ln 3 + ln 2.$
$ = 3ln 2 – frac{3}{2}ln 3$ $ = ln 8 – frac{3}{2}ln 3$ $ = 3ln frac{{2sqrt 3 }}{3}.$Bài 6. Tính $int_0^1 {{x^2}} {(1 – x)^5}dx$ bằng hai phương pháp:
a) Đổi biến số $u = 1 – x.$
b) Tích phân từng phần.Lời giải:
a) Đặt $u = 1 – x$ ta có: $du = – dx.$
Đổi cận:Ta có: $x = 1 – u$ nên:
$J = int_1^0 {(u – 1){u^5}du} $ $ = int_1^0 {{u^6}} du – int_1^0 {{u^5}} du$ $ = left. {frac{{{u^7}}}{7}} right|_1^0 – left. {frac{{{u^6}}}{6}} right|_1^0$ $ = frac{1}{{42}}.$
b) $J = – frac{1}{6}int_0^1 {xd} {(x – 1)^6}$ $ = – frac{1}{6}left[ {left. {x{{(x – 1)}^6}} right|_0^1 – int_0^1 {{{(x – 1)}^6}} dx} right].$
$ = – frac{1}{6}left[ { – int_0^1 {{{(x – 1)}^6}} d(x – 1)} right]$ $ = left. {frac{1}{{42}}{{(x – 1)}^7}} right|_0^1 = frac{1}{{42}}.$
Để lại một phản hồi